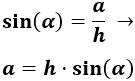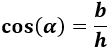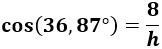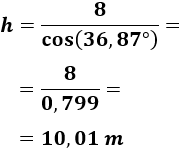Trigonométria del triangulo rectángulo Ejemplo

Trigonométria del triángulo rectángulo :

Calcula  el lado que falta en el triángulo rectángulo, si tiene cateto  a = 5 y b = 9.

Se debe averiguar C, la longitud de la hipotenusa.

Ángulos en coterminales Ejemplos (Positivos)

Ángulos en coterminales : Positivos ejemplo

Dibuja un ángulo positivo que sea coterminal a 60°

    

       Paso 1. Se calcula el ángulo coterminal y se dibujan en un mismo plano cartesiano.

                      

                                         60° + 360° = 420°

       

       Paso 2.  Se realiza lo mismo que en el ejemplo anterior.

                                

Ángulos en coterminales Ejemplos (Negativos)

Ángulos en coterminales : Negativos 

• Dibuja un ángulo negativo que sea coterminal a 45

      Paso 1.  Se resta 360°, o un múltiplo de él, de 45°.

                                 45° - 360° = -315°

      Paso 2.  Se dibuja 45° y -315° en un mismo plano cartesiano para comprobar que son                                       coterminales.

        

      

Funciones trigonometricas Ejemplo

Ejemplos de funciones trigonometricas

Calcular la altura, $a$, de un árbol sabiendo que, si nos situamos 8 metros de la base del tronco, vemos la parte superior de su copa en un ángulo de 36.87º.

Como la altura $a$ es el cateto opuesto al ángulo, utilizaremos el seno:

Pero como necesitamos calcular la hipotenusa $h$ del triángulo, utilizamos el coseno:

Sustituimos los datos:

La hipotenusa mide

Por tanto, la altura del árbol es

Sistema sexagesimal inverso Ejemplo

Sistema sexagesimal inverso Ejemplo

Como convertir un ángulo dado en grados con minutos y segundos en solo grados con decimales.
El método es muy simple: A los grados le sumamos los minutos divididos entre 60 y los segundo entre 3600 para finalmente obtener la medida del ángulo solo en grados con decimales

En este post se explicará de manera más detallada como convertir un ángulo con notación en grados con minutos y segundos en un ángulo con solo grados y decimales. Para lograr esto, debemos tener en cuenta las equivalencias que existen en este sistema de medidas (sexagesimal), como se explicó en posts anteriores un grado equivale a 60 minutos (1°=60´), un minuto equivale a 60 segundos (1´=60´´), o sea que un grado también equivaldría a tresmilseiscientos segundos (1°=3600´´). 

Haciendo uso de estas equivalencias se puede enunciar el siguiente mecanismo para convertir un ángulo con notación en grados con minutos y segundos en un ángulo con sólo grados y decimales: A los grados le sumamos los minutos divididos entre 60 y los segundos divididos entre 3600. Se pondrá el siguiente ejemplo: Convierta el ángulo 45°6´2’’ a un ángulo expresado sólo en grados con decimales. Como vemos la clave para resolver este problema es convertir los minutos y segundos en grados utilizando el mecanismo del enunciado, esto es 46° +1°( 6´/60´) +1°( 2´´/3600´´) = 45,10056°. Como vemos el ángulo quedo representado con grados y decimales

Sistema sexagesimal ejemplo

Sistema sexagesimal ejemplo

a) Convertir 18.4567 ° a Grados, Minutos y Segundos.

1. Como primer paso, tenemos que el número entero es de 18, éste nos equivale a 18°.

2. Luego los decimales después del punto es necesario que los pasemos a minutos, así:                                                       

OJO! Eliminamos unidades iguales y dejamos únicamente la que nos interesa, es decir, los minutos.

3. Ahora, tomamos los decimales 402 y los pasamos a Segundos. 0.402 ' x 60 '' (Segundos) = 24.12''

4. Ahora unimos todas las respuestas quedándonos 18 ° 27' 24'', que se lee: 18 Grados, 27 Minutos y 24 Segundos

NOTA: Si nos damos cuenta en cada conversión trabajamos sólo con los decimales, manteniéndose únicamente el primer número entero que corresponde a los Grados

Sistema Sexagesimal (INV)

 Sistema sexagesimal (INVERSO): 

 En este post veremos como resolver un problema de sistema sexagesimal a la inversa, 
 es decir de Gradosº Minutos' y Segundos" a Grados. 

Este tipo de problema se resuelve a través de una regla de tres simple.

Ejemplo:
  
15º 43' 48" a Grados

Se transforman los segundos a minutos: 
                                                            Una vez ya obtenido el resultado en minutos se suma.
 1'     60"
                    x=  48" * 1'   = 0.8' + 43' = 43.8'  
 x      48"               60"

Los minutos obtenidos se convierten a grados: 
                                                              Nuevamente se suma.
1º     60'                                                 
                 x=  43.8' * 1º  = 0.73º + 15º = 15. 73º 
x      43.8'               60'
                                                                 Respuesta 

Funciones trigonométricas OPUESTAS

Funciones Trigonométricas (Opuestas): 

Estos son los Inversos a las tres principales Funciones trigonométricas. 

Cosecante: Es el inverso de Seno.


 Su abreviación es CSC



Secante: Es el inverso se Coseno.


     Su abreviación es SEC



Cotangente: Es el opuesto de Tangente



Su abreviación es COT



                 
                    

Sistema Sexagesimal

Sistema Sexagesimal:  

El sistema sexagesimal es un sistema de numeracion posicional que emplea como base el número 60.  El sistema sexagesimal se usa para medir tiempos (horas, minutos y segundos) y ángulos (grados) principalmente.

Se representa asi:       Grados° Minutos´ Segundos" 

Para convertir una cantidad de Grados a Minutos y/o Segundos los Grados deben ser inexactos (Ej. 15.32°). 

Este proceso se lleva acabo a traves de una Regla de tres.

Por Ejemplo: 

 15.32° a sistema sexagesimal 

  Se tienen 15 grados exactos por lo que se convierte el 0.32 restante a minutos.

  1°         60´ 

                         x=       0.32° * 60'   =  19. 2' 

 0.32°      x                         1º 

  Se tienen 19 minutos exactos. con el 0.2 restante se calculan los segundos (") 

1'        60"

                      x=  0.2' * 60"    =  12" 

0.2'      x                     1'               

 Respuesta = 15º 19' 12"

Funciones Trigonometricas

FUNCIONES TRIGONOMÉTRICAS

Cada par de lados homólogos (que se ubican en la misma posición) de un triángulo rectángulo cuyos ángulos sean igualesserán proporcionales.

 Para que sea más fácil interpretar lo que se está explicando el típico triángulo de catetos de 3 cm y 4 cm, que tendrá su hipotenusa de 5 cm (Pitágoras). Dibujemos otros dos triángulos donde los catetos y la hipotenusa sean el doble y el triple (según corresponda).

Ahora Las Tres Funciones Basicas (sin Sus Inversos)

.

		Seno y la denotaremos por Sen(a)
		Coseno y la denotaremos por Cos(a)
		Tangente y la denotaremos por Tan(a)

Trigonometría del triangulo rectangulo.

           Trigonometría del triángulo rectángulo

• Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º.
• En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos.
Teorema de Pitágoras.- En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Demostración:

Si tenemos un triángulo rectángulo como el del dibujo del enunciado del teorema podemos construir un cuadrado que tenga de lado justo lo que mide el cateto b, más lo que mide el cateto c, es decir b+c, como en la figura de la derecha.
El área de este cuadrado será (b+c)².
Si ahora trazamos las hipotenusas de los triángulos rectángulos que salen tendremos la figura de la izquierda. El área del cuadrado, que es la misma de antes, se puede poner ahora como la suma de las áreas de los cuatro triángulos rectángulos azules (base por altura partido por 2):

más el área del cuadrado amarillo . Es decir, el área del cuadrado grande también es el área del cuadrado pequeño más 4 veces el área del triángulo:
Podemos igualar las dos formas de calcular el área del cuadrado grande y tenemos: si ahora desarrollamos el binomio , nos queda: que después de simplificar resulta lo que estábamos buscando:

Sistema Circular

                                  SISTEMA CIRCULAR

En este sistema se utiliza como unidad de medida el ángulo llamado “radián”.

Un radián es el ángulo cuyos lados comprende un arco cuya longitud es igual al radio de la circunferencia.  

Así, si la longitud del arco AB de la siguiente figura es igual a r, entonces ABC = 1 radián. 

Como el perímetro de cualquier circunferencia es 2 𝜋 r, resulta entonces que un ángulo de 360º equivale a 2𝜋r, es decir, si a 𝜋 se le asigna un valor de 3.1416 entonces 360° = 6.28 radianes, por lo que 1 radián = 360 / 6.28, quedando que 1radián = 57.3º.

Ángulos en coterminales

Ángulos en coterminales

Los ángulos coterminales son ángulos en posición estándar que tienen un lado terminal común. Por ejemplo 30°, –330° y 390°son todos coterminales.

Los angulos coterminales son aquellos que terminan exactamente donde terminan terminan otros ángulos, estos termina en el mismo cuadrante y no importando si son negativos o positivos

Ese es un ejemplo de ángulos coterminales, 150 y -210 son ángulos coterminales ya que los dos termina exactamente donde mismo, en el mismo cuadrante y posición

Ángulos con Los 4 Fantásticos + ratafak

Angulos

Un ángulo es la amplitud de rotación  o giro de un rayo alrededor de un punto fijo llamado vértice u origen

Tipos de Angulos

Existen diferentes tipos de angulos y estos se clasifican segun el rango en el que se encuentran, y estos rangos son:

Ángulo agudo:

 Mide menos de 90° y más de 0 °.

Ángulo recto:

 Mide 90° y sus lados son siempre perpendiculares entre sí.

Ángulo obtuso:

 Mayor que 90° pero menor que 180°.

Ángulo llano:

 Mide 180°. Igual que si juntamos dos ángulos rectos.

Angulos en la Trigonometria

Los ángulos trigonométricos a diferencia de los geométricos es que estos en cuestión son infinitos.Los ángulos trigonométricos se pueden considerar "positivos" y "negativos", la rotación de el vértice o también llamado origen es el que define si es positivo o negativo.

• Si la rotación va en sentido horario (En sentido de lasagujas del reloj) el ángulo se  considera negativo 

• O si va en sentido anti-horario (Al contrario de las agujas de reloj) este ángulo se considera positivo

Trigonometría con los 4 Fantásticos y ratafak

Trigonometría

Que es?
La trigonometria es una rama de la matematica la cual significa y se basa en la medicion de angulos. En terminos generales la "Trigonometria" es el estudio de las razones trigonometricas las cuales son: Seno, Coseno, Tngente, Cotangente, Secante y Cosecante.



En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno, coseno, tangente, cotangente, secante y cosecante. La trigonometría se aplica a otras ramas de la geometria, o la geometría analítica en particular geometría plana o geometria del espacio. En soluciones de ecuaciones diferenciales ordinarias, series de Fourier usadas en ecuaciones en derivadas parciales. Se usa en la mecánica.

Posee numerosas aplicaciones, entre las que se encuentran: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas globales de navegación por satélites.

La trigonometria abarca muchos temas muy importantes como Angulos, Angulos en posicion estandar ; Angulos Cotrminantes, Sistema Sexagecimal, Sistema Circularque seran explicados a detalle en este blog