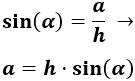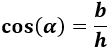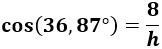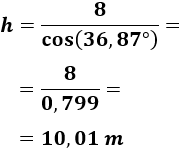Trigonométria del triangulo rectángulo Ejemplo

Trigonométria del triángulo rectángulo :

Calcula  el lado que falta en el triángulo rectángulo, si tiene cateto  a = 5 y b = 9.

Se debe averiguar C, la longitud de la hipotenusa.

Ángulos en coterminales Ejemplos (Positivos)

Ángulos en coterminales : Positivos ejemplo

Dibuja un ángulo positivo que sea coterminal a 60°

    

       Paso 1. Se calcula el ángulo coterminal y se dibujan en un mismo plano cartesiano.

                      

                                         60° + 360° = 420°

       

       Paso 2.  Se realiza lo mismo que en el ejemplo anterior.

                                

Ángulos en coterminales Ejemplos (Negativos)

Ángulos en coterminales : Negativos 

• Dibuja un ángulo negativo que sea coterminal a 45

      Paso 1.  Se resta 360°, o un múltiplo de él, de 45°.

                                 45° - 360° = -315°

      Paso 2.  Se dibuja 45° y -315° en un mismo plano cartesiano para comprobar que son                                       coterminales.

        

      

Funciones trigonometricas Ejemplo

Ejemplos de funciones trigonometricas

Calcular la altura, $a$, de un árbol sabiendo que, si nos situamos 8 metros de la base del tronco, vemos la parte superior de su copa en un ángulo de 36.87º.

Como la altura $a$ es el cateto opuesto al ángulo, utilizaremos el seno:

Pero como necesitamos calcular la hipotenusa $h$ del triángulo, utilizamos el coseno:

Sustituimos los datos:

La hipotenusa mide

Por tanto, la altura del árbol es

Sistema sexagesimal inverso Ejemplo

Sistema sexagesimal inverso Ejemplo

Como convertir un ángulo dado en grados con minutos y segundos en solo grados con decimales.
El método es muy simple: A los grados le sumamos los minutos divididos entre 60 y los segundo entre 3600 para finalmente obtener la medida del ángulo solo en grados con decimales

En este post se explicará de manera más detallada como convertir un ángulo con notación en grados con minutos y segundos en un ángulo con solo grados y decimales. Para lograr esto, debemos tener en cuenta las equivalencias que existen en este sistema de medidas (sexagesimal), como se explicó en posts anteriores un grado equivale a 60 minutos (1°=60´), un minuto equivale a 60 segundos (1´=60´´), o sea que un grado también equivaldría a tresmilseiscientos segundos (1°=3600´´). 

Haciendo uso de estas equivalencias se puede enunciar el siguiente mecanismo para convertir un ángulo con notación en grados con minutos y segundos en un ángulo con sólo grados y decimales: A los grados le sumamos los minutos divididos entre 60 y los segundos divididos entre 3600. Se pondrá el siguiente ejemplo: Convierta el ángulo 45°6´2’’ a un ángulo expresado sólo en grados con decimales. Como vemos la clave para resolver este problema es convertir los minutos y segundos en grados utilizando el mecanismo del enunciado, esto es 46° +1°( 6´/60´) +1°( 2´´/3600´´) = 45,10056°. Como vemos el ángulo quedo representado con grados y decimales

Sistema sexagesimal ejemplo

Sistema sexagesimal ejemplo

a) Convertir 18.4567 ° a Grados, Minutos y Segundos.

1. Como primer paso, tenemos que el número entero es de 18, éste nos equivale a 18°.

2. Luego los decimales después del punto es necesario que los pasemos a minutos, así:                                                       

OJO! Eliminamos unidades iguales y dejamos únicamente la que nos interesa, es decir, los minutos.

3. Ahora, tomamos los decimales 402 y los pasamos a Segundos. 0.402 ' x 60 '' (Segundos) = 24.12''

4. Ahora unimos todas las respuestas quedándonos 18 ° 27' 24'', que se lee: 18 Grados, 27 Minutos y 24 Segundos

NOTA: Si nos damos cuenta en cada conversión trabajamos sólo con los decimales, manteniéndose únicamente el primer número entero que corresponde a los Grados

Sistema Sexagesimal (INV)

 Sistema sexagesimal (INVERSO): 

 En este post veremos como resolver un problema de sistema sexagesimal a la inversa, 
 es decir de Gradosº Minutos' y Segundos" a Grados. 

Este tipo de problema se resuelve a través de una regla de tres simple.

Ejemplo:
  
15º 43' 48" a Grados

Se transforman los segundos a minutos: 
                                                            Una vez ya obtenido el resultado en minutos se suma.
 1'     60"
                    x=  48" * 1'   = 0.8' + 43' = 43.8'  
 x      48"               60"

Los minutos obtenidos se convierten a grados: 
                                                              Nuevamente se suma.
1º     60'                                                 
                 x=  43.8' * 1º  = 0.73º + 15º = 15. 73º 
x      43.8'               60'
                                                                 Respuesta